Ēlýsion pedíon

Irei, por meio desse texto, dar um exemplo do uso de matemática no mundo real. Todo estudante de ensino médio já deve ter se deparado com o seguinte circuito elétrico: Isto é um circuito de corrente alternada. Normalmente, num circuito elétrico queremos encontrar tanto a corrente em cada componente eletrônico e a tensão sobre os mesmos. Tendo esses valores, conseguimos calcular a potência gerada(ou consumida) por componente. A solução de um circuito como o da imagem é trivial e consegue ser obtida usando tanto as leis de Kirchhoff quanto a lei de Ohm. Interessante notar que para muitos estudantes, um circuito de corrente alternada é o primeiro exemplo físico onde se usa números complexos. Para facilitar as explicações, assumiremos nesse texto que o leitor sabe sobre Cálculo.

Resolver circuitos como o apresentado acima são tão fáceis que não tem o que comentar. Nesses tipos de problemas resolvidos na escola, sempre temos informações suficientes para resolver o problema. E, para facilitar nossa vida, acabam sendo equações lineares. Mas o que acontece quando o estudante decide resolver um sistema elétrico utilizado no mundo real, por exemplo:

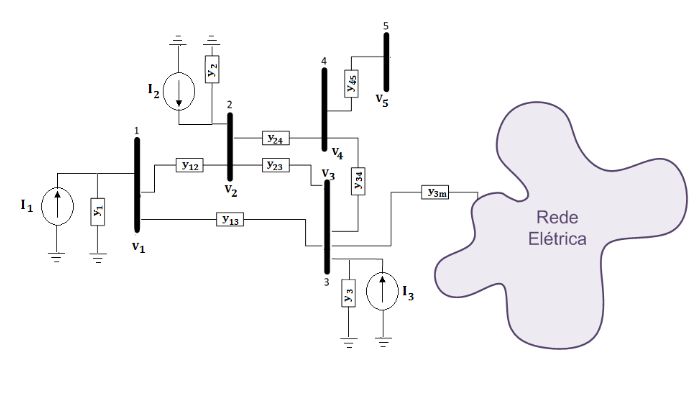
Não só é um circuito complexo como também não se tem informação o suficiente para resolver o problema usando as leis de Kirchhoff diretamente. Em termos matemáticos, temos mais variáveis que equações e não podemos chutar valores quaisquer aqui, pois teremos que checar se dada solução é válida(isto é, condiz com a realidade). Em outras palavras, chutar valores só tornaria as equações matemáticas resolvidas, mas não resolveria o problema real. Portanto, precisamos de novas equações para resolver o sistema.

Cada uma das barras na imagem acima (1, 2, 3, etc) são definidas por algumas propriedades que sabemos sobre elas. Uma barra $PV$ é assim dita pois sabemos a tensão naquela barra e a potência ativa dela, já uma barra $PQ$ é assim chamada pois sabemos tanto a potência ativa quanto a potência reativa. Existe um terceiro tipo de barra chamada de Swing(ou barra $V\theta$) que é uma barra de referência, calculada no fim para sabermos quais foram as perdas nas potências do sistema. Podemos usar as leis de Kirchhoff para calcular as potências ativa e reativa numa barra em função da tensão nas barras conectadas a ela, seus ângulos e também das admitâncias dos fios(isto é, as propriedades elétricas dos fios de transmissão de rede elétrica). Tais equações são:

$$P_{k}^{\text{calculado}} = V_{k}\Sigma_{m \in K}V_m (G_{km}\cos(\theta_{km}) + B_{km}\sin(\theta_{km}))\\ Q_{k}^{\text{calculado}} = V_{k}\Sigma_{m \in K}V_m (G_{km}\sin(\theta_{km}) - B_{km}\cos(\theta_{km}))$$

$K$ representa o conjunto de todas as barras no sistema, $G$ e $B$ são os elementos reais e complexos, respectivamente, de uma matriz $Y$ chamada de matriz de admitância. Tal matriz é formada com base nas propriedades elétricas dos fios. $G_{km}$ e $B_{km}$ são diferentes de $0$ se e somente se existe uma ligação entre as barras $k$ e $m$. Na maioria dos casos, tal ligação não existe e a matriz $Y$ acaba possuindo um monte de zero. Uma matriz com um monte de elementos $0$ é chamada de matriz esparsa. Já $\theta$ é o ângulo da tensão na barra e $\theta_{km} = \theta_k - \theta_m$.

Como mencionamos acima, existem barras que sabemos as potências ativas($PV$) e ambas as potências ativas e reativas($PQ$). Com isso, podemos criar equações para o nosso sistema. Para toda barra que sabemos as potências ativas($PV$), criamos a seguinte equação:

$$P^{\text{conhecido}}_k - P^{\text{calculado}}_k = 0$$

E para todas as barras que sabemos ambas as potências($PQ$), temos:

$$P^{\text{conhecido}}_k - P^{\text{calculado}}_k = 0\\ Q^{\text{conhecido}}_k - Q^{\text{calculado}}_k = 0$$

O objetivo é conhecermos os estados do sistema em cada barra, isso significa sabermos a tensão e o ângulo da tensão, pois com isso podemos calcular a corrente(Lei de Ohm nos dá isso, uma vez que $I = VY$, onde $I$ é a corrente, $V$ a tensão e $Y$ a admitância). Precisamos saber os ângulos das tensões por que tais ângulos são gerados num circuito de corrente alternativa e isso pode fazer com que uma corrente e a tensão não estejam em fases, isto é, estão defasados(o que influência na potência ativa que o sistema gera) e portanto devemos saber exatamente qual a defasagem no sistema. O caso onde sabemos a potência ativa e reativa só nos diz os valores para $P_k$ e $Q_k$, mas não para $V_k$ e $\theta_k$. Portanto, nas equações acimas, a maioria dos $V_k$ e $\theta_k$ são variáveis do qual NÃO sabemos os valores, as que sabemos entram como constantes na equação. E é exatamente essas variáveis que queremos calcular. O número de equações criadas depende do número e tipo de barras que temos. Para cada barra $PQ$ temos duas equações e para cada barra $PV$ temos uma equação, portanto são ao todo $2 * \#PQ + \#PV$ equações, onde $\#PQ$ é o número de barras $PQ$ e $\#PV$ é o número de barras $PV$. Para piorar as coisas, as equações criadas acima são equações não lineares.

Com as equações criadas, basta encontrar os valores de $V_k$ e $\theta_k$ que fazem o lado esquerdo das equações virarem $0$. Em matemática, isto é o mesmo que encontrarmos os valores onde a função se anula. Métodos para encontrar o $0$ de uma função, isto é, o ponto $x_s$ onde uma função $g(x)$ tem o valor $g(x_s)=0$ são chamados de “métodos para encontrar raízes de uma função”. Existem vários métodos e o que falarei agora, que é o mais usado nesse problema, é chamado de Método de Newton-Raphson. Um ótimo método para resolver sistemas de equações não lineares.

Seja o gráfico de uma função $g(x)$ a seguir: 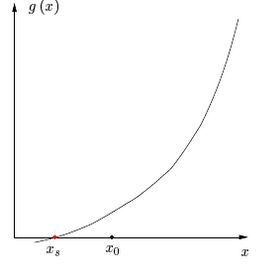Queremos encontrar o ponto $s$ tal que $g(s) = 0$. Escolhemos um ponto $x_0$ qualquer e calculamos $g(x_0)$. Se $x _0= s$, ótimo, mas isso nem sempre acontece. Então $g(x_0)$ será um ponto na curva. Pela derivada, podemos calcular a reta tangente ao gráfico no ponto $x_0$. Com isso, podemos ver onde a reta corta o eixo $x$. Essa localização é o nosso ponto $x_1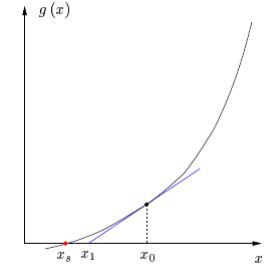$: Podemos repetir isso nos aproximando cada vez mais do ponto $s$. A ideia usada aqui é de um método iterativo, onde pelo método gera-se um ponto e tal ponto pode ser usado no método para gerar um novo ponto. Assim, podemos nos aproximar da solução apenas usando o ponto inicial e deixando o método gerar novos pontos. O método de Newton-Raphson é um exemplo de método iterativo.

A vantagem do método de Newton-Raphson é que ele gera o ponto novo calculando a reta e onde a reta corta o eixo $x$ ao mesmo tempo. Na verdade, ele nos dá a distância entre o ponto novo e o ponto atual, mas sabendo que $\Delta x = x_1 – x_0$, onde $\Delta x$ é a distância entre o ponto novo e o ponto atual, podemos calcular $x_1$ fazendo $x_1 = x_0 + \Delta x$.

Não mostrarei como se chega no método de Newton-Raphson, mas o mesmo pode ser feito usando aproximação linear da série de Taylor da função. A seguir temos o método de Newton-Raphson: $$\Delta x = -\frac{g(x)}{g'(x)}$$

Vale mencionar que o método raramente gera uma solução exata, mas sim uma solução aproximada. Uma solução exata nem sempre é possível, uma vez que a solução pode ser um número com casas decimais infinitas não repetidas. Mas o método pode gerar sempre uma solução aproximada, tão próxima quanto queremos. Isto é feito usando um valor $\epsilon$, chamado de tolerância, muito próximo de $0$ e tal que $x$ é solução se $|g(x)| \leq \epsilon$.

A imagem a seguir tem um exemplo do método sendo usado para encontrar uma solução: 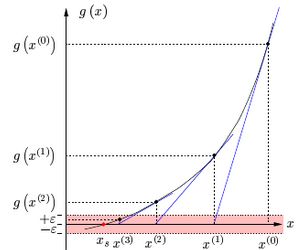Notamos que $x^{(3)}$ é uma solução pois $|g(x^{(3)})| \leq \epsilon$. Algo que ponde acontecer é que o valor inicial utilizado não gere uma solução(a reta tangente pode levar para um ponto cada vez mais longe de uma solução, por exemplo) e por isso devemos tentar outro valor inicial. Quando usamos um programa para gerar a solução, levamos em consideração um contador de iterações para terminar o método se depois de tantas iterações, uma solução não foi encontrada. Isso é uma indicação que o valor inicial não foi um bom chute.

No caso para $M$ variáveis, que é o caso considerado aqui, o método é muito parecido, a única diferença é que onde está a derivada da função, temos a matriz Jacobiana, $\mathbf{J}$, que é uma matriz com todas as derivadas parciais. Num sistema de $N$ equações com $M$ variáveis, teremos uma matriz $N \times M$ onde para cada equação(linha), temos $M$ derivadas parciais(colunas). O método possui a seguinte forma: $$\Delta x = -\mathbf{J}(x)^{-1} \cdot g(x)$$ Onde $\mathbf{J}(x)^{-1}$ é a inversa da matriz Jacobiana.

As equações mencionadas acima para $P$ e $Q$ são as equações que devemos derivar. As variáveis no caso são os $V_k$ e $\theta_k$. O nosso $\Delta x$ nesse caso é um vetor coluna formado por $\Delta V_k$ e $\Delta \theta_k$ e, por último, $g(x)$ são as equações para as barras $PV$ e $PQ$ mencionadas acima. Com isso, temos todas as ferramentas para calcular os estados, nossos $V_k$ e $\theta_k$, em todas as barras.

Mas é só isso? Na teoria, sim. Basta chutarmos valores iniciais e esperarmos o método gerar alguma solução. Em um computador, isso pode ser feito sem problemas (na verdade, existe um problema computacional em gerar a inversa da matriz Jacobiana, mas ignoramos isso aqui). Mas no mundo real isso não é o suficiente. Não entrarei muito em detalhes, pois aqui aparecem muitos problemas e vários jeitos de resolver isso, assim como grandes simplificações que podemos fazer com o que é conhecido sobre sistema elétrico. Mas comentarei sobre 2 importantes.

O primeiro problema é que a solução gerada para alguns $Q_k$ podem não condizer com a realidade. Numa barra $PV$, onde sabemos os valores da tensão e da potência ativa, podemos tentar calcular o valor da potência reativa naquela barra e descobrimos que o valore de $Q$ é maior ou menor que limites pré estabelecidos $Q_{max}$ e $Q_{min}$. Quando isso acontece, significa que a tensão naquela barra deve mudar (aumentar ou diminuir dependendo de que limite $Q$ passou). Como numa barra $PV$, a tensão é especificada, ela nunca muda quando novos pontos são geradas(isto é, ele não aparece nos $\Delta V_k$ acima), mas como o valor de $Q$ passou dos limites, é esperado que o valor de $V$ mude também. Para contornar esse problema, o que é feito é forçar a barra $PV$ virar uma barra $PQ$, tornando o valor de $Q$ conhecido o valor que $Q$ calculado ultrapassou, e forçando $V$ a virar uma variável do sistema. O que isso faz na equação é adicionar uma equação a mais (a do $Q$ dessa barra). A matriz Jacobiana acaba ganhando uma nova coluna(as derivadas parciais de cada equação em função dessa tensão $V$) e uma nova linha (as derivadas parciais da equação de $Q$ em função de cada variável). Feito isso, devemos checar se os valores de $V$ vão ser alterados como esperados(aumenta ou diminuem com base no valor de $Q$) e caso isso aconteça, mantemos a barra como $PQ$ até encontrar uma solução. Caso os valores de $V$ não sejam alterados como esperados, então devemos voltar para o caso da barra $PV$. Podemos entender isso como se alteramos a barra cedo demais, mas que os valores iriam se reestabelecer se tivéssemos mantidos as coisas e deixássemos o programa gerar a solução. Um jeito de evitar essa troca a toa é criamos uma tolerância $\sigma$ onde só nos importamos de checar o valor de $Q$ depois que o método gerou novos pontos tais que $|g(x)| \leq \sigma$.

O segundo problema é para barras $PQ$. Os valores de $V$ gerados nela podem passar de limites pré estabelecidos $V_{max}$ e $V_{min}$. Neste caso, mudamos de uma barra $PQ$ para uma barra $PV$. O que foi dito acima sobre voltar ou não pode ser repetido aqui.

A pergunta que fica é: por que desejamos calcular isso? Bom, a resposta é planejamento. Suponha que queremos instalar novas barras para levar energia elétrica para novas regiões. Para isso, precisamos saber se as novas barras afetarão drasticamente o sistema existente ou não. Isto é, se terá algum problema em instalar as novas barras. O método utilizado acima nos dá uma boa ideia de onde pode haver problemas, se a queda de tensão numa parte é além do esperado, se haverá grandes perdas nas potências, se a potência reativa gerada em uma barra pode afetar demais o sistema, etc. Fazendo os cálculos, vemos facilmente se podemos instalar as novas barras ou se devemos fazer alguma mudança no sistema para pôr as novas barras.

Com isso, temos um exemplo do uso da matemática(e física) no mundo real.

#math