In this article I’ll explain how I wrote a Hex board game on Python. This article is more important for me, as it’s nice to have written down what you did to solve some problem. The source code is here and commits shows what went through my head as I wrote the program.
For those that have not heard about this game, the link above explains the game. In short, the game is played in a NxN (usually 11x11) rhombus board composed of NxN hexagons cells. Each player takes a turn placing one hexagon piece on the board and the objective is to connect both sides of the same color as the hexagon pieces the player is using, so the red hexagon player has to connect the both red sides and the blue hexagon player has to do the same for the blue sides). The first to connect wins.
Since the idea is to connect sides, it was obvious that the algorithm that I was going to use was a depth-first search and so I had to use a graph to represent the game. To simplify things, I started with a 2x2 game, which looks like:

So I created a 2x2 matrix representing the game, the numbers above represent positions in a matrix, and a dictionary to represent a graph. Whenever a player placed a piece, we would add that piece’s position to his graph. And so, starting in a 2x2, whenever we placed two pieces, the player would win. Obviously, the algorithm would work as it didn’t connect any edges in our graph, any piece placed would be added to the player's graph and that would be enough to check if from any position we could get to some position, which would be always true as that position would be part of the player’s graph. Looking at the image above, if the red player placed a piece at position 0 and 3, he wouldn’t be able to win as the pieces are not connected, but it worked for the algorithm, which was enough to show the first problem, as explained above.
So came the first problem, which was to how connect pieces in the board so that we do have a connection before checking if any pĺayer won the game.First I focused on how connect the pieces, and the solution was to create a function that given a piece’s position, we generate all its neighbors and so we check to see if any of its neighbors has any position occupied by a piece so we could connect them. The function that generates the neighbors of a piece was good enough that it would work even if we increased the board size. So it was one less problem to care about when we tested for 3x3 board size, since in this case we could introduce more problems; just because something works for the simple case, it doesn’t mean it will work for the not-so-simple case, it does however help to restrict the problem more, it’s less thing to taken into account as you solve the problem.
Well, connecting pieces in the board was a good idea, however, I had not taken into account that we need to check if any piece was owned by the same player as the one played at the moment and because of that, we could have any of the players winning because as long as the player could reach both ends, it didn’t matter if it was not by connecting only pieces of the same color. Thus, I had to create a dictionary to store each player's pieces. This way we would connect two pieces only if they were owned by the same player. I still need to fix the original problem of not adding all the pieces in each player’s graph, but now it is easier. Given that I have a dictionary that takes into account what pieces each player owns and a graph showing the pieces connected, I only need to see if any of the pieces on one side of the board can connect to the other side for each player. So I only added to each player’s graph the pieces in one of the sides, the left side for the red player and the upper side for the blue player. When a player places a piece, the piece is added to the graph, then if it’s in the left/upper side of any player, the initial positions, we also add the piece to that player’s graph and finally we check the neighbors of the piece to connect the pieces in the graph. Doing this, the algorithm to check if the sides connect would only see if the pieces in the player’s graph can connect to the other side.
After that, I created a simple main function to check if the game was working even if I tried a 11x11 board. Since it worked, I decided to change the command line version with pygame.
At this point, it was just using the pygame’s function to finish the game. The interesting thing is that at some point, while I was making the graphic version, I found out that the matrix was not necessary anymore, so I removed it. The graphs were doing all the work, I only needed to re-use the idea of each place in the board having a numeric representation to help me generate the neighbors of a piece.
And here we have the game playing:
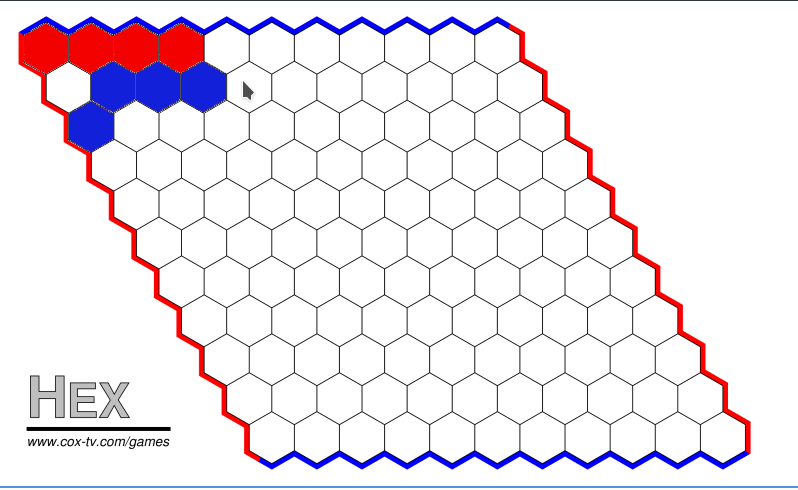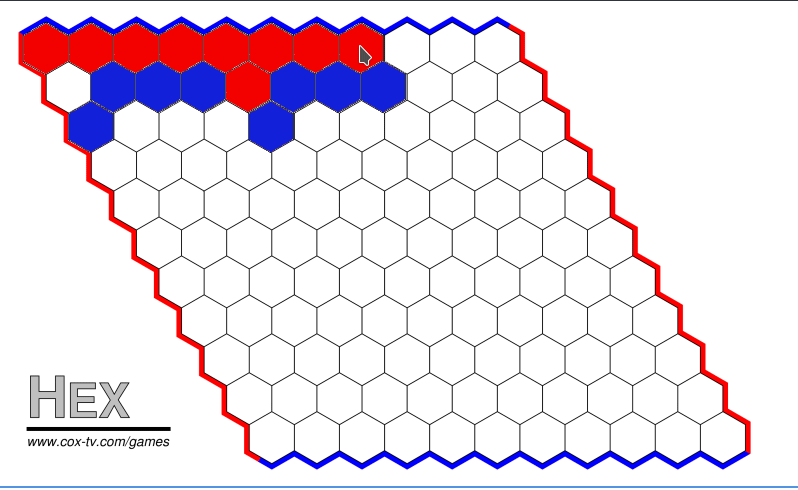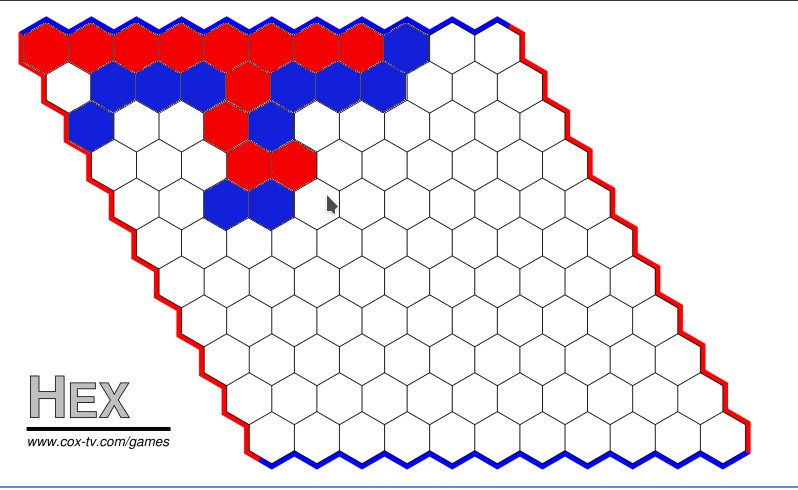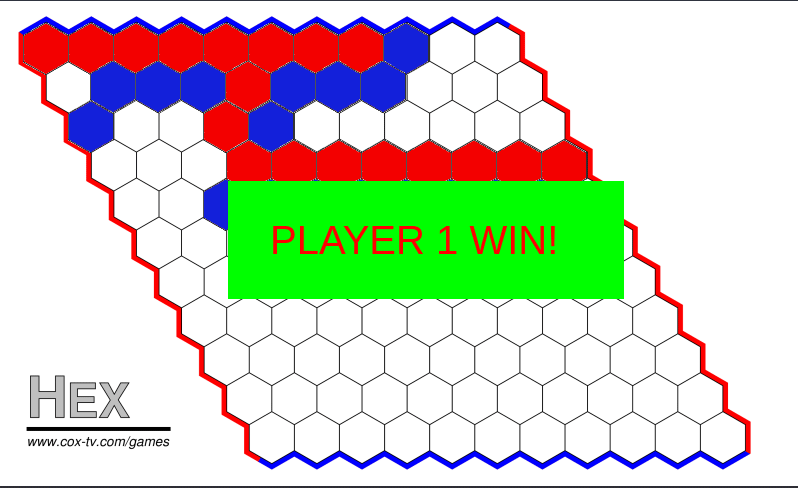
That is how I wrote it. As I said above, I believe this is more useful to me than for anyone that is trying to learn how to code it, thankfully anything that I explained badly or forgot to mention can be seen in the commits, so this article and the commits will be the best comments I could get out of my code.
Right now I’m learning the basics of network programming to make the game multiplayer to play with a friend, after that I’ll study the basics of game AI to make an AI opponent.